Plastic number
| List of numbers – Irrational and suspected irrational numbers γ – ζ(3) – √2 – √3 – √5 – φ – ρ – δS – α – e – π – δ |
|
| Binary | 1.0101001100100000101… |
| Decimal | 1.32471795724474602596… |
| Hexadecimal | 1.5320B74ECA44ADAC1788… |
| Continued fraction[1] | 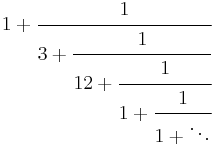 Note that this continued fraction is not periodic. |
| Algebraic form | ![\sqrt[3]{\frac{1}{2}%2B\frac{1}{6}\sqrt{\frac{23}{3}}}%2B\sqrt[3]{\frac{1}{2}-\frac{1}{6}\sqrt{\frac{23}{3}}}](/2012-wikipedia_en_all_nopic_01_2012/I/77868e7cfd04e8765651a9b8397d273c.png) |
In mathematics, the plastic number ρ (also known as the plastic constant) is a mathematical constant which is the unique real solution of the cubic equation
It has the value[2]
its decimal expansion begins with 1.324717957244746025960908854....
The plastic number is also sometimes called the silver number, but that name is more commonly used for the silver ratio 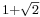 .
.
Contents |
Properties
The powers of the plastic number A(n) = ρn satisfy the recurrence relation A(n) = A(n − 2) + A(n − 3) for n > 2. Hence it is the limiting ratio of successive terms of any (non-zero) integer sequence satisfying this recurrence such as the Padovan sequence and the Perrin sequence, and bears the same relationship to these sequences as the golden ratio does to the Fibonacci sequence and the silver ratio does to the Pell numbers.
Because the plastic number has minimal polynomial x3 − x − 1 = 0, it is also a solution of the polynomial equation p(x) = 0 for every polynomial p that is a multiple of x3 − x − 1, but not for any other polynomials with integer coefficients.
The plastic number satisfies the nested radical recurrence:[3]
The plastic number is the smallest Pisot–Vijayaraghavan number. Its algebraic conjugates are
of absolute value ≈ 0.868837. This value is also 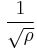 because the product of the three roots of the minimal polynomial is 1.
because the product of the three roots of the minimal polynomial is 1.
History
The name plastic number (het plastische getal in Dutch) was given to this number in 1928 by Dom Hans van der Laan. Unlike the names of the golden ratio and silver ratio, the word plastic was not intended to refer to a specific substance, but rather in its adjectival sense, meaning something that can be given a three-dimensional shape.[4] This is because, according to Padovan, the characteristic ratios of the number, 3/4 and 1/7, relate to the limits of human perception in relating one physical size to another.
Notes
- ^ Sequence A072117 in the OEIS.
- ^ Sequence A060006 in the OEIS.
- ^ Piezas, Tito III; van Lamoen, Floor; and Weisstein, Eric W., "Plastic Constant" from MathWorld.
- ^ Padovan (2002);Shannon, Anderson & Horadam (2006).
References
- Gazalé, Midhat J. (1999), Gnomon, Princeton University Press.
- Padovan, Richard (2002), "Dom Hans Van Der Laan And The Plastic Number", Nexus IV: Architecture and Mathematics, Kim Williams Books, pp. 181–193, http://www.nexusjournal.com/conferences/N2002-Padovan.html.
- Shannon, A. G.; Anderson, P. G.; Horadam, A. F. (2006), "Properties of Cordonnier, Perrin and Van der Laan numbers", International Journal of Mathematical Education in Science and Technology 37 (7): 825–831, doi:10.1080/00207390600712554.
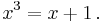
![\rho = \sqrt[3]{\frac{1}{2}%2B\frac{1}{6}\sqrt{\frac{23}{3}}}%2B\sqrt[3]{\frac{1}{2}-\frac{1}{6}\sqrt{\frac{23}{3}}};](/2012-wikipedia_en_all_nopic_01_2012/I/7cf5304711b0492c74880668bc56750a.png)
![\rho = \sqrt[3]{1 %2B \sqrt[3]{1 %2B \sqrt[3]{1 %2B \cdots}}} \, .](/2012-wikipedia_en_all_nopic_01_2012/I/6e3fba0b5c4c1b06b07c9bcb91d86ee8.png)
![\left(-\frac12\pm\frac{\sqrt3}2i\right)\sqrt[3]{\frac{1}{2}%2B\frac{1}{6}\sqrt{\frac{23}{3}}}%2B\left(-\frac12\mp\frac{\sqrt3}2i\right)\sqrt[3]{\frac{1}{2}-\frac{1}{6}\sqrt{\frac{23}{3}}}\approx -0.662359 \pm 0.56228i
,](/2012-wikipedia_en_all_nopic_01_2012/I/34b388aa33dc475c37cbbb8698ef464d.png)